eの計算 パターン2
フェルマーの小定理を使ったちょっとした問題
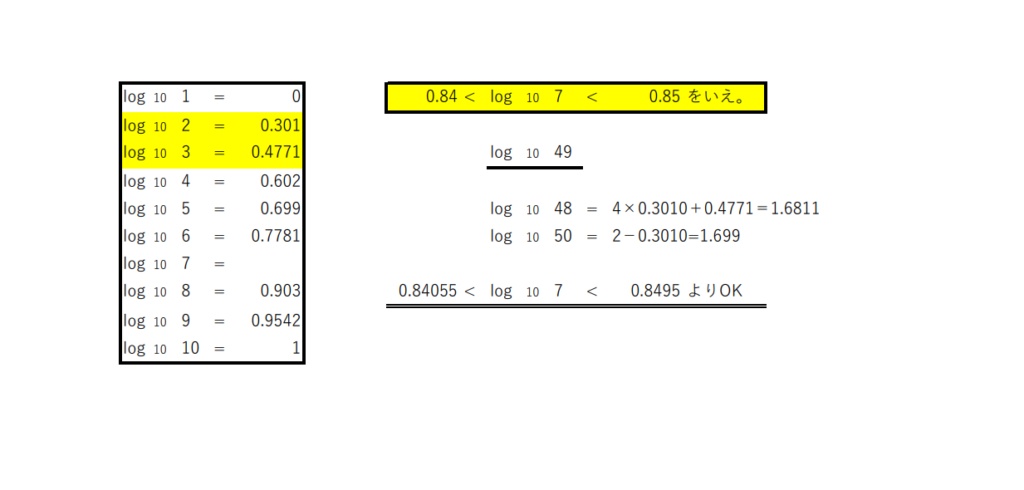
log 10 7の値を評価しよう
log101からlog1010の値は、基本 log102と log103で表現できるが、 log107だけは、うまくいかない。しかし、工夫をすれば、不等式を使って評価できる。
ド・モアブルを利用した問題
cosの積
5777を2乗+2乗の形に2通りで表現してみよう
→ただし、5777=53×109 の素因数分解は既知としよう
ネイピア数e を Π(円周率) 乗 したら 22 より大きくなる?
tanθの7乗の定積分
ある数の一の位


コメント
新ネタです。ネイピア数eの値を定積分と数列から算出した面白いアプローチとなつてます。階乗を使って表現できる過程がよくわかります。
フェルマーの小定理を使った問題を加えました。4乗を6乗や10乗などにかえても全然対応できる問題です。おそるべし定理です。
対数の問題増やしました。
ド・モアブルを利用した問題をアップしました。
5777を素因数分解ができていれば、2乗和で2通りに表すことが簡単にできます。面白い問題です。
e(ネイピア数)のΠ(円周率)乗は22よりおおきい。結構簡単に確認できます。つなみに実際は23よりおおきいです。
タンジェントの定積分の問題です。漸化式を利用します。
ジャイアンツは大失速。CS進出もあやうい?おもしろい問題みつけました。一の位を求めます。mod10を使いますが、一工夫必要です。
ヤクルト、オリックス ペナントレース優勝おめでとうございます。ジャイアンツは来年投手を整備して日本一を目指しましょう。原監督続投らしいです。